中华文明历史悠久，中华文化博大精深、源远流长，中国古代数学也一样有着辉煌的成就。华罗庚先生说过，中华民族是最擅长数学的。作为微积分学的基础的极限理论直到19世纪才得以完善，但是极限思想的萌芽可以追溯到大约两千五百年前，在中国和西方都展现出了极限的思想。而我国是世界上最早产生极限思想和应用极限思想的国家。

早在春秋战国时代（公元前770——前221），《庄子·天下篇》 中有这样一句：“一尺之棰，日取其半，万世不竭”。意思就是说：一尺长的一根木棒，如果每天截下一半，永远都取不完，这样的过程可以无限地进行下去。另外，在《墨子·经下》中有也有一句：“非半弗斫，则不动，说在端。”这句话的意思是说，一条线段从中点分为两半，取其一半冉破成两半，仍取一半继续分割，直到不可分割时就只剩下一个点。这些体现出了古人对无限思想的认识，蕴含了朴素的、直观的极限思想。

魏晋时期（公元3世纪），我国的数学家刘徽在《九章算术注》中写到：“以六觚之一面乘半径，因而三之，得十二觚之幂。若又割之，次以十二觚之一面乘半径，因而六之，则得二十四觚之幂。割之弥细，所失弥少。割之又割，以至于不可割，则与圆合体，而无所失矣。”这里“觚”是正多边形，“面”是正多边形的边，“幂”是正多边形的面积。刘徽的方法就是先做一个圆内接正六边形，然后平分每组对边的弧，作出圆的内接正十二边形，同样的方法继续作圆的内接正二十四边形、四十八边形……正多边形的边数越多，即所谓“割之弥细”，圆的面积与正多边形的面积相差就越少。当分割次数无限增加，也就是正多边形的边数无限增大时，正多边形将与圆重合。用我们今天的说法就是圆内接正多边形面积的极限即为圆面积。这就是刘徽著名的割圆术，割圆术是极限思想在几何上的应用。

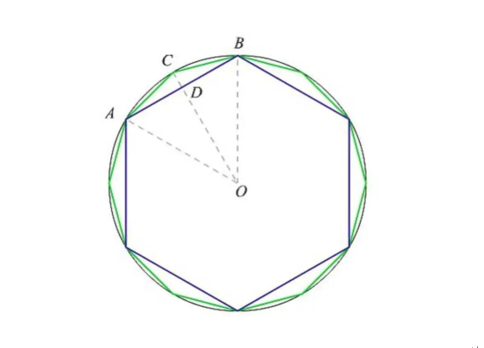
祖率在西方直到1573才由德国人奥托得到，1625年发表于荷兰工程师安托尼斯的著作中，欧洲称之为安托尼斯率。祖冲之的圆周率保持了千年之久，直到 15 世纪才被阿拉伯数学家阿尔·卡西打破 , 计算到小数点后 17 位。

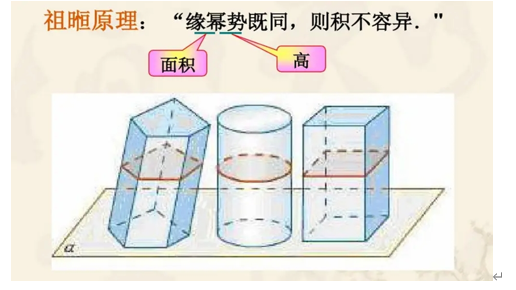
祖冲之和他的儿子祖暅编写了一本名为《缀术》的专著，这本书在唐代初期被选作国子监算学馆的教材之一。据说《缀术》的内容十分艰深、是唐朝算学中最难的课本，所以习者寥寥。在北宋元丰七年（1084年）时‚便已经失传，非常可惜。《缀术》中有云：“缘幂势既同，则积不容异”。意思是说：如果两个立方体的所有等髙的横截面积全都相等， 那么这两个立方体的的体积一定是相同的。这正是“不可分量”思想的延续。这个原理我们称之为“祖暅原理”，在微积分里被西方称为卡瓦列里（Cavalieri）原理。祖暅原理的发现比卡瓦列里原理早1000 多年。 祖暅承袭了刘徽的思想，利用祖暅原理求出“牟合方盖”的体积，进而利用“牟合方盖”求出了球体的体积，解决了刘徽所遗留的问题。

《缀术》代表了当时数学的最高水平价值，但是由于已经失传，我们无法得知其内容。有学者认为《缀术》中会蕴含极限思想，因为“缀” 本身字就有“连续”之含义。

刘徽、祖冲之都是我国历史上杰出的科学家。他们的科学发现与创造是我国古代科技发展成就的重要代表之一，他们的研究对于人类社会的发展做出了极 大的贡献，他们的卓越贡献对世界都有着深刻的影响。

本文只是介绍了中国古代数学成就中关于极限思想的一小部分，中国古代数学的成就远远不止于此。在悠久的历史长河中，我们有先进的科技文化，有无数卓越的数学家，我们曾是数学领域的领跑者。虽然今天，在某些方面我们略有落后，但是只要有信心、不放弃、勇攀登，相信我们必然会崛起！

作者：殷红燕；编辑：胡军浩；审核：李海涛；上传：刘鹍。